Träd Datastrukturer
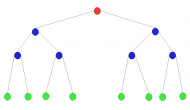
Träd är en vanlig abstrakt datatyp eller datastruktur som lagrar element i en hierarkisk träd struktur, som liknar ett arvsträd.
Träd består av ett root element som har ett subträd av barn med en förälder nod. Det representeras som länkade noder, precis som med en länkad lista. Fast noderna har länkningar till mer än bara nästa. I denna artikeln kommer vi kolla på två binära träd, Heap och Binary Search Tree.
#Förutsättning
Du kan grunderna i Python och objektorientering. Du har jobbat igenom övningen exceptions och Datastrukturer.
#Binära träd/Binary Tree
För definitionen av träd kan ni kolla in Preliminary definition på Wikipedia, kolla på bilderna och dess texter.
I Binära träd har varje nod max två barn noder, vilket betyder att icke-binära träd kan ha flera barn noder. Det är samma koncept, bara det att ens kod behöver ha koll på flera noder i varje nod. Tänk er en länkad lista med fler referenser.
En nod klass för ett binärt träd kan se ut på följande sätt:
class Node():
def __init__(self, key, value, parent=None):
self.key = key
self.value = value
self.parent = parent
self.left = None
self.right = None
#Heap
Heap är ett specialiserat träd där förälder noden har ett värde som antingen är högre eller lägre än sin barn. Om föräldern alltid är högre kallas det en Max Heap och om det är mindre heter det en Min Heap.

Max heap.
Varje cirkel representeras av en nod (Node) som har en referens till sin förälder och två barn. Noden “30”, key är 30, har exempelvis en referens till förälder noden “75”. Om ni vart uppmärksamma på bilden så har ni märkt att varje barn nod har ett värde som är lägre än föräldern, detta är för att det är en Max Heap på bilden. Det innebär att root noden i trädet innehåller det högsta värdet som finns sparat i strukturen och varje nods barn har lägre värde än sig själv.
Max Heap och Min Heap kallas även för PriorityQueue, då vi kan använda dem för att skapa en prioriterad kö. Om vi alltid plockar ut root elementet kommer man alltid få ut det värde som har högst eller minst värde i strukturen. Då blir det som en kö fast istället för First in First out beror det på vilket värde man har, eller prioritet som det kallas.
När man lägger till ett värde i en Heap läggs värdet sist/längst ner. Sen jämförs det med sin förälder. Är det nya värdet mindre så blir det ett barn till den föräldern. Är det nya värdet större kommer barnet ta förälderns plats och en ny jämförelse sker på nästa förälder. På så sätt kommer alltid det största värdet vara i toppen, i “roten”. Man lägger alltid till nya värden sist för att hålla trädet balanserat och med så få nivåer som möjligt.
#Lägga till
Stegen som tas för att lägga till värden är:
1. Lägg till element i den lägsta nivån.
2. Jämför värdet med föräldern. Är föräldern större, stanna.
3. Annars byt plats på dem och upprepa steg 2.
Vi lägger till värdet “80”:
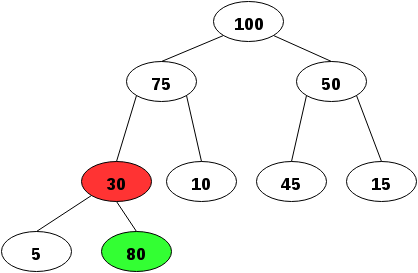
80 är större än sin förälder, 30. De ska då byta plats:
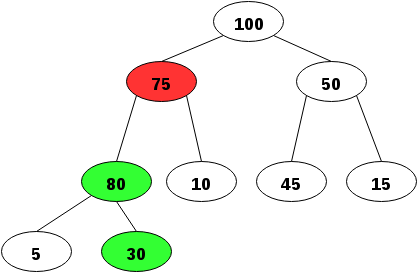
Samma gäller för nästa förälder. 80 är större än 75, så de ska byta plats:

80 är mindre än 100 så nu ligger det nya värdet på rätt plats. Om vi lägger till ett nytt värde nu så hamnar det till vänster under noden “10”. Det har skett en så kallad “inplace”-sortering.
#Ta bort värde
När man extraherar ett värde från heapen tar man alltid roten, i detta fallet det största då det är en max-heap.
Stegen som tas för att ta bort ett värde är:
1. Byt ut roten mot sista elementet på den sista nivån.
2. Jämför den nya roten med sina barn. Är barnen mindre, stanna.
3. Annars byt plats med det största barnet och upprepa steg 2. (Byt med minsta barnet i en min-heap)
Vi tittar på hur det kan se ut:
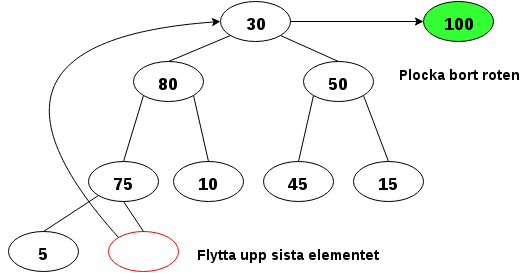
30 är mindre än båda sina barn så vi byter plats med det största barnet:
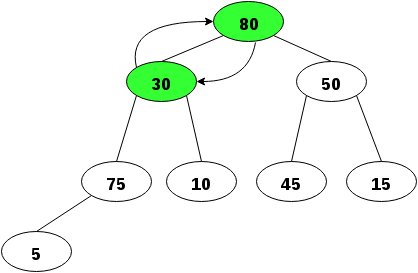
Ett barn är mindre så vi skiftar plats:
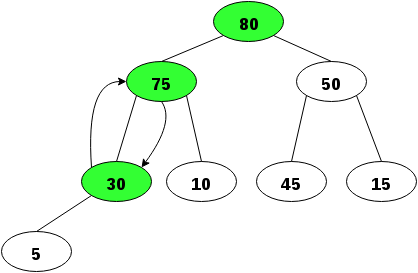
Nu håller trädet måttet för att kallas en max-heap. Om vi skulle haft en min-heap istället hade det varit det minsta värdet i roten.
#Binary Search Tree
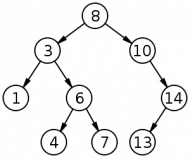
Binary search tree med storleken 9, djupet 3 och roten 8.
Eller Binära sök träd (bst), är en effektiv datastruktur som passar för att spara data med nycklar, som en dictionary, associative array, table eller map. Bst sparar nycklarna i sorterad ordning, de är sorterade så att det vänstra barnet alltid är lägre än föräldern och det högra barnet alltid är större. Till skillnad från en Heap så så utgår man från trädets rot och strukturen beror på vilken ordning noderna läggs in. Det första värdet som stoppas in kommer att vara root noden tills den tas bort och blir då ersatt med det lägsta värdet på höger sida av trädet.
Trädets sortering låter oss oftast “klippa bort” hälften av alla grenar varje nod som traverseras, är t.ex. värdet vi letar efter (eller vill stoppa in) lägre än rotens värde ignorerar vi höger sidan av noden, går ett steg till vänster och jämför med nästa nod.
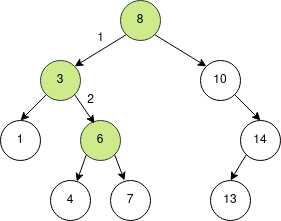
Bst som söker efter värdet 6.
Operationer som get, insert och delete får då en proportionerligt tid av logaritmen av antalet noder i trädet, O(log n). Det blir bättre än en länkad lista som tar linjärt med tid men det är långsammare än arrayer och Hash tables.
Är man inte försiktig finns det risk att trädet kan bli skevt och dess operationer kommer att få sämre prestanda. I det värsta fallet får den tids komplexiteten O(n) istället för O(log n). Bilden nedanför visar hur ett skevt träd kan se ut. Följande kod genererar ett skevt träd:
bst = BinarySearchTree()
bst.insert(10, "tio")
bst.insert(20, "tjugo")
bst.insert(30, "trettio")
bst.insert(40, "fyrtio")
bst.insert(50, "femtio")
Det läggs bara in högre nycklar och får då inga noder till vänster. Trädet blir då likadant som en länkad lista.
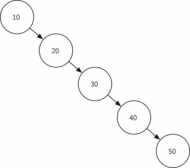
Höger skevt bst.
#Mer info om BST
Kolla på CS50 Data structures från tidsstämpeln fram till 01:14:26, för en snabb förklaring av träd och Binary Search Tree och jobba sen igenom slides:en i VisuAlgo Binary Search Tree, fram till och med “kapitel” 13.
Läs sen om de olika sätten man kan travesera noder i ett träd.
#Avslutningsvis
Nu har vi kollat på ytterligare en sort av datastrukturer, träd, mer specifikt Heap och Binary Search Tree. Det finns en till vanlig typ av datastruktur, Hash tables, vilket är den snabbaste datastrukturen för key/value data.
Ni kan läsa följande två länkar Find k-th smallest element in BST (Order Statistics in BST) och A program to check if a binary tree is BST or not om ni är intresserade.
#Revision history
- 2019-02-20: (A, aar) Första versionen.