Rekursion

Med rekursion menas en funktion som anropar sig själv. Antingen direkt eller via en annan funktion. Det handlar om ett annat tankesätt än vad vi är vana vid, till exempel for-loopar och andra iterativa och linjära tankesätt.
#Förutsättning
Du kan grunderna i Python och du vet vad variabler, typer och funktioner innebär.
#The Three Laws of Recursion
Rekursion har tre lagar (The Three Laws of Recursion):
En rekursiv funktion måste ha ett basfall, något som kontrollerar hur många gånger den upprepas.
En rekursiv funktion måste ändra sitt tillstånd och arbeta sig mot basfallet
En rekursiv funktion måste kalla på sig själv, rekursivt.
En viktig sak att tänka på är att det är lätt att hamna i ett “infinite” läge. Tänk dig följande kod som är tänkt att summera alla heltal från 1 till n:
def recursive_sum(times):
# Här kallar vi på funktionen rekursivt
return n + recursive_sum(times-1)
Den kommer aldrig sluta snurra, då vi inte har ett basfall. Vi behöver en tröskel där det tar stopp och rekursionen avslutas:
def recursive_sum(times):
# Här är basfallet. När times kommer till 1 så returneras bara värdet.
if times <= 1:
return times
# Vi ändrar tillståndet och jobbar oss mot basfallet
sum_so_far = times + recursive_sum(times-1)
print(sum_so_far)
return sum_so_far
>>> recursive_sum(5)
3
6
10
15
Nu har vi ett basfall, if n <= 1:, som stoppar de rekursiva anropen, vi har ett tillstånd, times, som ändras mot basfallet,times-1, och vi har ett rekursivt anrop, sum_so_far = times + recursive_sum(times-1).
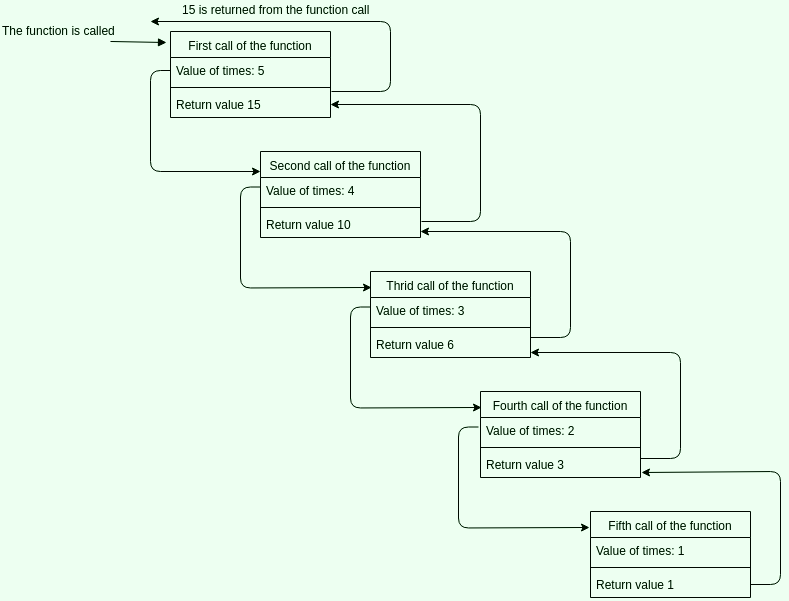
Värdet av times och retur värdet för varje funktionsanrop.
Bilden visar varför en rekursiv algorithm måste reducera ett problem för varje rekursiva anrop. Rekursionen måste stanna för att lösningen ska ärknas ut.
Funktionen uppfyller alla 3 krav. Ett tips är att alltid börja implementera basfallet för att förhindra ett infinite-läge.
Antalet gånger en rekursiv funktion anropar sig själv kallas för the depth of recursion. Funktionen ovanför med argumentet 5 har djupet fem. När funktionen anropas den femte gången har times värdet 0 och då inträffar basfallet.
#Varför rekursion?
Om man ska använda rekursion eller inte beror på olika faktorer. Som med allt annat så finns det fördelar och nackdelar jämfört med en iterativ funktion.
#Fördelar
- Rekursiva funktioner gör att koden blir renare.
- En komplex uppgift kan brytas ner till små problem.
- Beroende på problem kan det vara enklare med en rekursiv funktion.
#Nackdelar
- Rekursiva funktioner tar upp mer minne.
- Rekursiva funktioner är ofta långsammare.
- Rekursiva funktioner är svårare att debugga.
- Rekursiva funktioner kan vara svåra att förstå.
#Typer av rekursion
#Linear recursion
“Linear recursion” är när en rekursiv funktion kallar på sig själv en gång varje gång funktionen körs. Det är den vanligaste modellen av en rekursiv funktion.
#Tail recursive
“Tail recursion” är en form utav Linear recursion. Det rekursiva anropet är det sista som görs i funktionen, vilket gör att den passar bra för iterativa funktioner. Om man byter ut det rekursiva anropet mot en loop kan samma resultat uppnås.
#Binary recursive
“Binary recursions” har två eller fler rekursiva anrop i funktionen.
#Avslutningsvis
Rekursion kan vara en ovärderlig struktur, vid rätt tillfälle. Oftast klarar man sig bra med vanliga loopar men med den här vetskapen finns i alla fall alternativet till hands.
#Revision history
- 2017-02-08: (A, lew) First version.